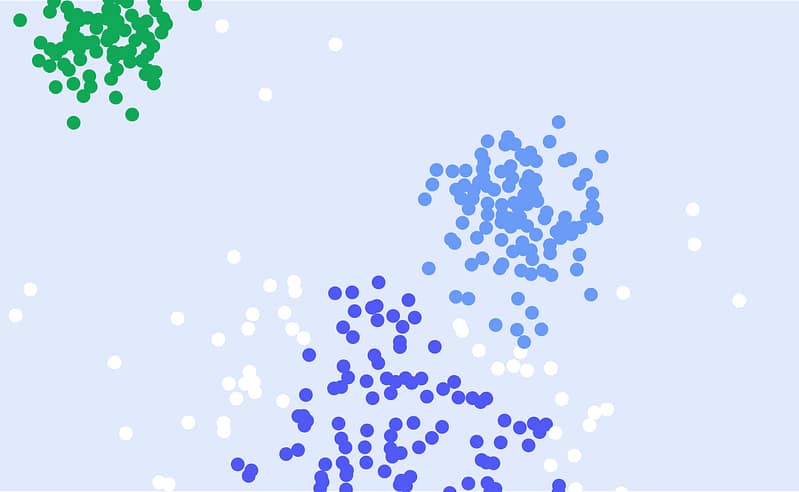
Cluster Analysis is a useful tool used to identify patterns and relationships within complex datasets. It involves using algorithms to group data points into groups called clusters. Grouping data points based on their similarities and differences allows researchers to gain insights into the underlying structure of their data.
Table of Contents
- Introduction to Cluster Analysis
- Types of Cluster Analysis
- Which Cluster Analysis to Use When?
- Data Preparation for Cluster Analysis
- Interpreting and Visualizing Cluster Analysis Results
- Common Mistakes and Disadvantages of Cluster Analysis
- Principal Component Analysis and Cluster Analysis
- Future Directions in Cluster Analysis Research
- Resources and Tools for Cluster Analysis
Cluster analysis has a wide range of applications in various fields, including marketing, biology, finance, and social sciences. For example, it can be used to identify genetic markers associated with specific diseases, to detect anomalies in financial transactions, and to classify social media users into different categories based on their interests and behaviors. It is commonly used in market research for segmenting customers into groups based on their buying behaviors.
This page will provide a comprehensive guide to cluster analysis, covering the different techniques and algorithms used in the process, best practices for conducting cluster analysis on big data, common challenges and how to overcome them, and real-world case studies demonstrating the application of cluster analysis in practice.
Cluster analysis in 2025: Whether you are a researcher, data or insights analyst or consultant, it is important to have a tool that can aid in the clustering process. Try this cluster analysis template in Displayr.
Introduction to Cluster Analysis
Definition and purpose of cluster analysis
Cluster analysis is a statistical technique in which algorithms group a set of objects or data points based on their similarity.
The result of cluster analysis is a set of clusters, each distinct from the others but largely similar to the objects or data points within them.
The purpose of cluster analysis is to help reveal patterns and structures within a dataset that may provide insights into underlying relationships and associations.
Applications of cluster analysis
Cluster analysis has a huge range of applications across different fields and industries. Here are some common examples:
- Image Processing: In image processing, cluster analysis groups pixels with similar properties together, allowing for the identification of objects and patterns in images.
- Biology and Medicine: Cluster analysis is used in biology and medicine to identify genes associated with specific diseases or to group patients with similar clinical characteristics. It can help with disease diagnosis and treatment.
- Social Network Analysis: In social network analysis, cluster analysis groups individuals with similar social connections and characteristics together, allowing for the identification of subgroups within a larger network.
- Anomaly Detection: Cluster analysis can detect anomalies in data, such as fraudulent financial transactions, unusual patterns in network traffic, or outliers in medical data.
Cluster Analysis Algorithms
There are several different types of cluster analysis, as thousands of algorithms have been developed that attempt various ways to group objects into clusters. This guide will cover some of the main ones:
K-means clustering
K-means clustering is a method that groups data points into a predetermined number (k) of clusters based on their distances to the centroid of each cluster. This is an iterative algorithm that aims to minimize the sum of squared distances between data points and their assigned cluster centroids.
K-means cluster analysis follows these steps:
- Specify the number of clusters. This is referred to as k. Normally, researchers will conduct k-means several times, exploring different numbers of clusters as the starting point.
- Allocate objects to clusters. The most straightforward approach here is to randomly assign objects to clusters.
- Compute cluster means. For each cluster, the average value is computed for each of the variables.
- Allocate each observation to the closest cluster center.
- Repeat steps 3 and 4 until the solution converges.
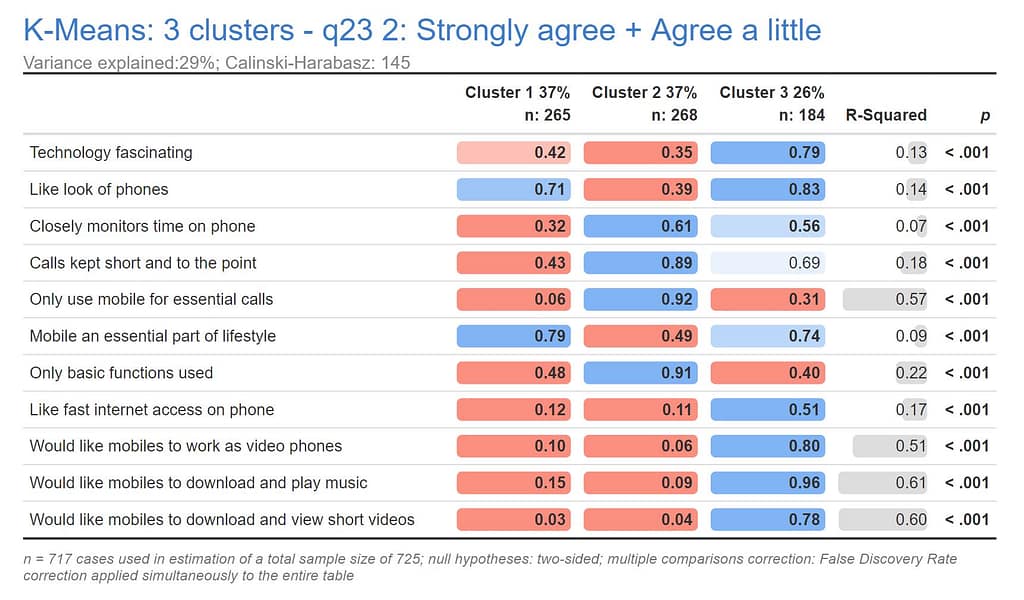
Model-based clustering
Model-based clustering assumes that the data points within each cluster follow a particular probability distribution. This method is often used when the underlying data distribution is not well-known or when the data contains noise or outliers.
Density-based clustering
Density-based clustering groups data points together based on their density within a defined radius or distance threshold. It is useful for identifying clusters with irregular shapes or clusters that are widely separated.
Fuzzy Clustering
Fuzzy clustering is a method that assigns each data point a membership score for each cluster, rather than a binary membership value. This type of clustering is useful when data points can belong to more than one cluster simultaneously or when there is uncertainty about which cluster a data point belongs to.
Which Cluster Analysis to Use When?
With so many different clustering techniques, it can be challenging to determine which method to use. The following table provides a brief summary on the recommended cluster analysis method based on the objective, as well as key considerations for each technique:
| Data Characteristics/Objective | Recommended Cluster Analysis Method | Key Considerations |
|---|---|---|
| Data points form well-defined, spherical clusters; you know (or want to test) a specific number of clusters (k). | K-means Clustering | – Sensitive to initial centroid placement; run multiple times. – Assumes clusters are spherical and equally sized. – Requires specifying the number of clusters (k) beforehand. – Good for large datasets due to its efficiency. |
| You assume your data follows a specific probability distribution (e.g., Gaussian, Poisson) within each cluster; you want to account for statistical likelihood. | Model-based Clustering | – Requires assumptions about the underlying data distribution. – Can handle clusters with varying shapes and sizes. – Useful for handling noise and outliers. – Can estimate the optimal number of clusters based on statistical models. |
| You want to identify clusters with irregular shapes or varying densities; you want to find clusters in noisy data. | Density-based Clustering | – Effective for finding clusters of arbitrary shapes. – Robust to outliers. – Doesn’t require specifying the number of clusters beforehand (can be determined automatically). – May struggle with datasets where densities vary significantly across clusters. |
| Data points can belong to multiple clusters simultaneously; you want to represent uncertainty or overlap in cluster assignments. | Fuzzy Clustering | – Allows for partial membership of data points in clusters. – Useful when cluster boundaries are not well-defined. – Provides a degree of membership for each data point in each cluster. – More complex to interpret compared to hard clustering methods. |
Data Preparation for Cluster Analysis
There are some important steps to consider when preparing your data for cluster analysis.
Data cleaning and transformation
Before performing cluster analysis, it’s important to ensure that the data is clean and free from errors. This may involve removing missing values, outliers, or duplicates.
You may also need to get your data in the right format. Typically, cluster analysis is performed on a table of raw data, where each row represents an object and the columns represent quantitative characteristics of the objects. These quantitative characteristics are called clustering variables.
For example, in market segmentation, where k-means is used to find groups of consumers with similar needs, each object is a person and each variable is commonly a rating of how important various things are to consumers (e.g., quality, price, customer service, convenience).
Cluster analysis can also be performed using data in a distance matrix.

Handling missing values
Most cluster analysis software or algorithms will not work with missing values in the data, so you will want to handle any missing values immediately.
There are five main options for dealing with missing data when using cluster analysis. They are: complete case analysis, complete case analysis followed by nearest-neighbor assignment for partial data, partial data cluster analysis, replacing missing values or incomplete data with means, imputation.
Complete case analysis
Complete case analysis involves using only data points with complete information in the analysis – any data points that contain missing values are removed.
However, this approach assumes that the data is Missing Completely At Random and that the missing values have the same characteristics as the cases with complete data. Unfortunately, this is almost never true in reality. By removing data with missing values, the size of the dataset is reduced and may result in problems such as a bias in the clustering results.
Complete case analysis followed by nearest-neighbor assignment for partial data
The complete case analysis followed by nearest assignments for partial data follows the same approach as complete case analysis but with the added step of assigning the remaining observations to the closest cluster based on the available data.
Partial data cluster analysis
Partial data cluster analysis involves grouping observations together based on the data they have in common.
Replacing missing values with means
Another way of dealing with missing data is to replace missing values with the mean value of that variable.
Imputation
Another approach is to impute or estimate the missing values. One form of imputation is the same as the method above – mean imputation. But there are other forms, such as regression imputation (using regression models to predict missing values) or k-nearest neighbor imputation (using the values of the nearest neighbors to estimate missing values).
Scaling and normalization
If the variables in the data have different scales, it’s important to normalize or standardize them so that they have similar ranges. This can help prevent variables with larger scales from dominating the clustering process.
Although, scaling, normalization and standardization are related terms, they do not mean the same thing. Normalization refers to the process of changing the values of numeric columns in the dataset to a common scale. Standardization refers to changing the feature values, while the shape of the distribution doesn’t change.
Feature selection
Depending on the complexity of the data, it may be necessary to select a subset of the most relevant features to include in the clustering analysis. This can help reduce noise and improve the quality of the clustering results.
Interpreting and Visualizing Cluster Analysis Results
Cluster profiles and characteristics
Looking at the profile and characteristics can help you interpret the results. Calculate and display the mean or median values of the variables within each cluster. This helps you identify the characteristic features of each cluster and understand their differences. You can visualize the cluster profiles using bar plots, line plots, or radar charts.
Cluster visualization techniques (scatterplots, heatmaps, dendrograms)
You can also use various data visualizations to interpret your cluster analysis results.
Scatterplots can help you visualize the data points and their assigned cluster labels by showing you the grouping patterns and the separation between clusters. Each data point is represented as a dot, and the different clusters are distinguished by different colors or symbols.
You can also use heatmaps to visualize the similarity or dissimilarity between data points and clusters. A heatmap displays a color-coded matrix, where each cell represents the distance or similarity measure between a data point and a cluster centroid. This visualization helps you identify which data points belong strongly to a particular cluster.
Dimensionality reduction techniques
Applying dimensionality reduction techniques, such as principal component analysis (PCA) or t-SNE, can assist you to visualize the clusters in a lower-dimensional space. This can help reveal complex relationships and separations between clusters that are not easily visible in the original high-dimensional data.
Common Mistakes and Disadvantages of Cluster Analysis
Here are some common mistakes with cluster analysis to avoid.
Overfitting and underfitting
In cluster analysis, overfitting refers to the phenomenon where a clustering algorithm creates clusters that are overly complex or intricate, fitting the noise or idiosyncrasies of the data rather than capturing the underlying patterns or structure. Overfitting can occur when the algorithm has too much flexibility or when the number of clusters is too large compared to the intrinsic structure of the data.
Signs of overfitting in cluster analysis may include:
- Clusters that appear excessively fragmented or contain only a few data points.
- Clusters that exhibit irregular shapes or boundaries that do not align with the underlying structure of the data.
- Extremely fine-grained clusters that do not provide meaningful insights.
Underfitting in cluster analysis also means that the clustering algorithm has failed to capture patterns or the structure of the data adequately, but in this case it occurs when the chosen algorithm or settings are too rigid or simplistic to capture the complexity of the data.
Signs of underfitting in cluster analysis may include:
- Clusters that are overly generalized and fail to capture meaningful subgroups or distinctions.
- Inadequate separation between clusters, making it difficult to interpret or differentiate them. Clusters that do not align with known patterns or expectations in the data.
Underfitting can result in oversimplified or incomplete representations of the data.
Selection bias
One of the common mistakes or disadvantages to using cluster analysis is selection bias. When using hierarchical clustering, you need to make certain decisions when specifying both the distance metric and the linkage criteria. Unfortunately, there is rarely a strong theoretical basis for these decisions and such, can be described as arbitrary decisions. These decisions can lead to selection bias, which in turn leads to skewed or inaccurate clustering results.
Here are some scenarios where selection bias can occur in relation to cluster analysis:
- Non-random sampling: If the data used for clustering is collected through non-random sampling methods, such as convenience sampling or self-selection, it may introduce biases. For example, if participants self-select to be part of a study, their characteristics or behaviors may differ from those who did not volunteer, leading to biased clusters.
- Missing data bias: One disadvantage of cluster analysis is that most hierarchical clustering software will not work if you have missing data. However, if missing data is not handled appropriately, it can introduce selection bias. If certain individuals or variables have missing values that are not missing completely at random (MCAR), the clustering results may be distorted, as the missing data patterns could be related to the underlying cluster structure.
- Cluster selection bias: In hierarchical clustering, where clusters are formed through a stepwise merging process, the order in which the clusters are combined can impact the final results. If the order is biased or predetermined based on specific criteria, it can introduce selection bias and affect the resulting clusters.
- Exclusion of certain groups: If certain groups or subpopulations are excluded or underrepresented in the data used for clustering, the resulting clusters may not adequately capture the full diversity or patterns in the population. This can lead to incomplete or biased insights.
Principal Component Analysis and Cluster Analysis
When it comes to complementary techniques for cluster analysis, principal component analysis (PCA)/factor analysis (they are technically different techniques, but the difference is minor) sits atop the list.
In essence, this is because PCA reduces the dimensionality of data by transforming correlated variables into smaller sets of uncorrelated principal components that maintain most of the variance. This means PCA is ideal for clustering datasets with many variables.
Using these complementary techniques also improves the quality of the clusters formed. By uncovering latent factors or principal components, PCA/factor analysis ensures that the variables used in the clustering process are more meaningful and less redundant, resulting in better-defined and more interpretable clusters.
For instance, in a dataset with consumer preferences, PCA can highlight the underlying factors (e.g., price sensitivity, brand loyalty) that differentiate customer segments. Once these factors have been identified, cluster analysis can group consumers based on these more relevant dimensions, providing more actionable insights.
Future Directions in Cluster Analysis Research
Advancements in clustering algorithms
Researchers are continuously working on developing and improving clustering algorithms to address various challenges and data types. Some areas of advancement include:
- Robustness to high-dimensional data: As data dimensionality increases, clustering algorithms that can effectively handle high-dimensional data while preserving meaningful structures are being explored. Techniques such as subspace clustering, ensemble clustering, or sparse clustering are being developed to address this challenge.
- Scalability and efficiency: With the increasing size of datasets, scalable clustering algorithms are being developed to handle big data efficiently. Methods such as distributed clustering, online clustering, or parallel clustering algorithms are gaining attention to address scalability concerns.
Integration with other machine learning techniques
Cluster analysis is often combined with other machine learning techniques to improve the overall analysis and obtain more actionable insights. One integration direction includes integrating clustering with deep learning techniques. Approaches like deep clustering and autoencoders are being explored to combine deep learning and clustering.
Emerging applications and areas of research
Cluster analysis is finding applications in various domains, and researchers are exploring new areas of application and conducting domain-specific studies. Some emerging areas of research include:
- Healthcare and precision medicine: Clustering techniques are being used to identify patient subgroups, disease patterns, or personalized treatment approaches. Clustering is aiding in precision medicine initiatives by enabling better patient stratification and disease subtype discovery.
- Social network analysis: Clustering algorithms are employed in social network analysis to identify communities or detect influential nodes. Research focuses on developing algorithms that capture the dynamic nature of social networks and consider multiple network attributes.
- Anomaly detection and cybersecurity: Clustering techniques are used for anomaly detection, identifying outliers, or detecting network intrusions. Researchers are working on developing clustering algorithms that can handle complex and evolving threats in cybersecurity.
- Image and video analysis: Clustering methods are applied to image and video data for tasks such as image segmentation, object recognition, or video summarization. Research focuses on developing algorithms that can handle large-scale image and video datasets efficiently and capture complex visual patterns.
These are just a few examples of the future directions in cluster analysis research. As data and technology continue to evolve, cluster analysis will play a vital role in extracting meaningful information and insights from complex datasets across various domains.
Resources and Tools for Cluster Analysis
Software and programming languages for cluster analysis
Displayr
Displayr is an all-in-one analysis and reporting software purpose-built for researchers. It makes it easy to perform hierarchical clustering, k-means clustering, latent class analysis, and all the associated techniques for predicting class membership in new data sets (e.g., regression, machine learning). Displayr also automatically deals with missing data problems using the best-practice MAR assumption.
ClustVis
ClustVis is a web-based tool designed for visualizing clustering of multivariate data using principal component analysis (PCA) and heatmaps. Users can easily upload their data, select clustering and visualization options, and instantly generate interactive plots that highlight patterns and groupings within the data. The tool supports both row and column clustering.
R
R is a popular open-source programming language and environment for statistical computing and data analysis. It provides a wide range of packages and libraries designed for cluster analysis, such as “stats,” “cluster,” “fpc,” and “dbscan.” R offers a comprehensive set of functions for performing various clustering algorithms, evaluating cluster validity, and visualizing clustering results.
Python
Python is a versatile programming language with a rich ecosystem of libraries and tools for data analysis and machine learning. The “scikit-learn” library in Python provides numerous clustering algorithms, including k-means, hierarchical clustering, DBSCAN, and more. Python also offers libraries like “scipy” and “numpy” that provide additional functions and tools for cluster analysis.
MATLAB
MATLAB is a proprietary programming language and development environment commonly used in scientific and engineering applications. It offers a wide range of functions and toolboxes for cluster analysis, including clustering algorithms, cluster validation metrics, and visualization capabilities. The Statistics and Machine Learning Toolbox in MATLAB provides several clustering algorithms and tools.
SPSS
SPSS (Statistical Package for the Social Sciences) is a software package for statistical analysis. It offers several clustering algorithms, including k-means, hierarchical clustering, and two-step clustering.
Data sources and datasets for practice
If you’d like to explore more about cluster analysis, you can try it yourself for free using Displayr or explore these examples of hierarchical cluster analysis on different datasets using R.
Learning resources
Looking to learn from more real-world applications of cluster analysis? You can explore how to use cluster analysis for market segmentation with this eBook on How to do Market Segmentation or webinar on DIY Market Segmentation.